Моделирование нестационарных процессов в турбомашинах на основе нелинейно-гармонического NLH-метода с использованием суперкомпьютеров
Ю.Я. Болдырев, А.О. Рубцов, Ю.В. Кожухов, А.А. Лебедев, И.В. Чеглаков, А.М. Данилишин
Целью работы является апробация нелинейно-гармонического метода NLH (Non-linear harmonic), предназначенного для моделирования нестационарного аэродинамического взаимодействия ротора и статора в турбомашинах, отличающегося высокой скоростью вычислений в сравнении с подходами полномасштабного нестационарного расчёта течения. Расчеты нестационарных течений в турбомашинах относятся к классу вычислительно ресурсоемких задач и для решения реальных задач за приемлемое время требуется использование суперкомпьютеров. На кафедре «Компрессорной, вакуумной и холодильной техники» в целях апробации получены решения двухмерных и трёхмерных течений в турбомашинах с применением NLH метода, реализованного в программном комплексе NUMECAFine/Turbo. К настоящему времени проведено сравнение нестационарного течения со стационарным, получены картины течений и рассмотрен вопрос о консервативности параметров течения.
Введение
В проектировании турбомашин необходимо учитывать нестационарные процессы для обеспечения надежной работы машин и установок. В осевых и центробежных компрессорах работа в области малой производительности может приводить к вращающемуся срыву, так называемому помпажу – локальной и глобальной потери устойчивости течения, соответственно. Также могут возникать такие аэроупругие явления как, например – флаттер. Указанные нестационарные процессы ведут к появлению вибраций, повышенного шума, дополнительных динамических напряжений в элементах проточной части, что может привести к серьезной поломке и аварии турбомашины. Следует указать и на то обстоятельство, что в осевых турбомашинах играет значение, и так называемый нестационарный клокинг-эффект (Сlocking-effect- эффект тактовой синхронизации), позволяющий повысить КПД машины за счет взаимодействия двух последовательно расположенных роторов или статоров с одинаковым числом лопаток в лопаточных венцах.
Проведение нестационарных исследований на экспериментальных стендах достаточно дороги и требуют значительной квалификации исследователя. Однако с появлением передовых вычислительных методов моделирования турбулентности класса URANS (Unsteady Reynolds average Navie-Stoks) стоимость численного эксперимента оказывается на порядок ниже натурного. Такие численные исследования проводились на кафедре «Компрессорной, вакуумной и холодильной техники» (КВиХТ) [1] на суперкомпьютере. Так для нестационарного расчета полной окружности рабочего колеса и безлопаточного диффузора центробежного компрессора потребовалось 30 234 880 элементов расчетной сетки, при этом использовалось 6 вычислительных узлов кластера, с 24 вычислительными ядрами и 32 Гб RAM. Расчет только на режиме вращающегося срыва потребовал 14000 итераций и занимал порядка 12 суток. В связи с этим очевидно, что проблема времени расчета значительно обострится при моделировании течений для полных многоступенчатых нестационарных процессах в турбомашинах с учетом всех междисковых зазоров и лабиринтных уплотнений, а также подводящих и отводящих газ камер.
В настоящее время существует два подхода снижения времени расчета: во-первых — это увеличение вычислительных ресурсов для решения данного класса задач; и, во-вторых, — это применение новых подходов к их численному решению.
В рамках первого подхода в Политехническом университете Петра Великого создается Суперкомпьютерный центр, с суммарной пиковой вычислительной мощностью около 1 Pflop/s..
Далее мы остановимся на одном из наиболее перспективных вариантов численного решения рассматриваемого класса задач, основанного на представленных в 1996 году в работах [2, 3] по методу нелинейных гармоник (NLH). Этот метод обеспечивает приближенное решение нестационарных задач при существенном уменьшении объема вычислений.
Математическая основа NLH метода
Изначально метод NLH разрабатывался для моделирования течений в межлопаточном пространстве в турбомашинах. Течение в таком случае считается квази-трехмерным, а именно оно разбивается на слои, в каждом из которых считается двумерным. Областью решения является подпространство вращающихся декартовых координат, при этом частота вращения совпадает с частотой ротора рассматриваемой турбомашины. Предполагается, что течение описывается уравнениями Навье-Стокса движения вязкой жидкости, которые будучи записаны в интегральной форме в случае квази-трехмерного приближения на движущейся поверхности ∆A имеют вид:
(1)
здесь символом S обозначен контур поверхности ∆A,
— вектор переменных состояния,
, — вектора конвективных потоков,
— вектор внешних воздействий, и — скорости движения расчетной сетки, следующей за вращением и вибрацией лопаток. Векторные слагаемые, учитывающие эффекты вязкости (вязкие члены) имеют вид
,
где, …, соответствующие компоненты тензора скоростей деформаций и вектора потока тепла, выражающиеся формулами:
(2)
Для замыкания системы уравнений необходимо определить значение давления, которое в случае идеального газа находится из формулы:
,
где Cp и Cv известные постоянные. Динамическая вязкость μ, входящая в уравнения для напряжений (2) представляется как обычно в виде суммы ламинарной и турбулентной вязкостей: . Ламинарная вязкость рассчитывается исходя из закона Сазерленда, а турбулентная – из стандартной алгебраической модели Болдуина-Ломакса. Коэффициент теплопроводности рассчитывается из значения динамической вязкости μ из равенства для числа Прандтля: .
Ключевым предположением метода является допущение о том, что течение может быть разделено на две составляющие: стационарный поток и малые возмущения.
(3)
Аналогично, в таком виде представляются вязкие члены, координаты узлов расчетной сетки и скорости движения расчетной сетки.
После подстановки полученных представлений для всех величин в форме (3) в уравнение (1) и осреднения его по времени имеем:
(4)
Заметим, что обычно, амплитуда движения узлов сетки для задач расчета течения в турбомашинах относительно невелика и можно пренебречь дополнительными слагаемыми, содержащими нестационарную составляющую координат узлов сетки.
(5)
Если подставить те же представления величин в форме (3) в уравнение (1) и вычесть осредненную по времени составляющую в виде уравнения (5) получим соотношение для нестационарных колебаний:
(6)
Члены второго порядка, входящие в слагаемые этого уравнения, предполагаются пренебрежительно малыми и исключаются из рассмотрения.
Далее используется метод гармоник, в рамках которого традиционно
нестационарные возмущения потока представляются в виде:
, (7)
где — вектор амплитуд переменных сохранения. Координаты узлов расчетной сетки и её скорости также представляются в гармоническом виде. Подставляя выражения вида (7) в (6) получаем следующее уравнение:
(8)
Показывается [2, 3], что для численного решения полученных уравнений (5) и (8), необходимо привести их к гиперболическому виду. Для этого вводится переменная псевдовремени t′ и проводится замена переменной t. Следует заметить, что для решения осредненного по времени уравнения (5) необходимы дополнительные уравнения. Такими уравнениями выступают выражения, связывающие так называемые «нестационарные напряжения», которыми являются выражения для турбулентных пульсаций вида , входящие в состав конвективных потоков, со значениями амплитуд и фаз нестационарных колебаний, получаемых из уравнения для гармонических колебаний для первой гармоники следующего вида
(9)
Для n-гармоник имеем:
(10)
При этом для совместного решения уравнений (5) и (8) используется, так называемый, метод сопряжения с сильной связью. В этом методе уравнения (5) и (8) решаются одновременно, с использованием схемы Рунге-Кутта 4-ого порядка.
Как отмечалось в отличие от других современных математических моделей, применяемых для расчета нестационарных течений, в которых решается трехмерная задача, метод нелинейных гармоник позволяет перейти к квази-трехмерной, которая, по сути, представляется собой набор двумерных задач. За счет такого подхода в методе NLH решение задач идет гораздо быстрее, при этом мы получаем высокую точность результатов. Однако, как и в случае трехмерных нестационарных моделей, для того, чтобы решать реальные задачи, необходимо использовать высоко — качественные расчетные сетки, состоящие из большого числа элементов. При этом следует учитывать и то естественное обстоятельство, что в методе NLH число выбранных (рассчитываемых) гармоник Np сильно влияет как на точность получаемых результатов, так и на необходимые вычислительные ресурсы. Из-за этого применение суперкомпьютерных технологий является важным аспектом при использовании данного метода.
Некоторые результаты
К настоящему времени на кафедре «Компрессорная, вакуумная и холодильная техника» накоплен определенный опыт практического применения метода NLH, реализованного в программном комплексе NUMECAFine/Turbo [4] для двухмерных и трёхмерных течений вязкого газа в турбомашинах. В целях апробации возможностей метода NLH были проведены расчеты двухмерных течений в цилиндрических вырезах высотой в одну расчетную ячейку для турбинной ступени и компрессорной осевой ступени, состоящей из статора, ротора и статора.
В турбинной ступени рассматривалась проницаемость энтропии через межсеточную границу между вращающимся неподвижным лопаточным аппаратом и рабочим колесом и определялось значение КПД в зависимости от количества гармоник Np. Повышение энтропии показывает распределение низкоэнергетических зон в газе, таких как вихревые зоны и места схода газа с лопаток. На рисунке 1 слева показана картина распределения энтропии при расчёте с 3 гармониками, заметна низкая консервативность параметра. На рисунке справа показано распределение энтропии при расчёте с 10 гармониками, с заметно лучшим сохранением значений поля энтропии при прохождении через межсеточную границу. Это подтверждается графиком на рис. 2, на котором заметны побочные явления метода: возникновение паразитных возмущений, которые тем меньше, чем больше гармоник используется в расчёте. Расчёты сравнивались по адиабатному КПД:
, (10)
где — полная и статическая температура на входе и выходе из расчетной области, а — газодинамическая функция; — коэффициент скорости — скорость звука, — коэффициент изоэнтропы, R – универсальная газовая постоянная, Т— температура.
Расхождения по КПД для расчёта с тремя гармониками составили — 0,23% по сравнению со стационарным решением, и — 0,18% для расчёта с 10 гармониками.

Рис.1. Распределение энтропии на роторе и статоре через межсеточную границу при 3 (слева), 10 (справа) гармониках
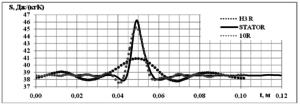
Рис.2. Проницаемость энтропии через межсеточную границу. Чёрная линия – Энтропия перед границей (STATOR), чёрный пунктир – энтропия при расчёте с 3 гармониками со стороны ротора (H3 R), серый пунктир – 10 гармоник, со стороны ротора (10R).
В компрессорной ступени с высоконагруженными сверхзвуковыми лопатками было отмечено изменение режима течения на рабочих лопатках: метод NLH в осреднённой картине течения показал менее интенсивное распределение скоростей и иное положение скачка уплотнения в сравнении с расчётом в стационарной постановке. Сравнить картины распределения числа Маха в относительном движении можно на рисунке 3: слева – стационарное решение, справа – решение методом NLH. Различие по политропному КПД составило 0,5% между решениями.

Рис. 3. Распределения числа Маха в относительном движении, стационарное решение
Также была рассчитана промежуточная малорасходная ступень центробежного компрессора высокого давления (рис. 4), в которую входит рабочее колесо, безлопаточный диффузор, поворотное колено и обратно-направляющий аппарат. Расчеты показали, что нестационарность, инициируемая рабочим колесом (точка 2), падает на два порядка к концу безлопаточного диффузора (точка 4). Данный эффект был неоднократно замечен экспериментально в ходе работ на кафедре КВиХТ. На рисунке 4 показано сечение ступени с положением контрольно-измерительных точек, в которых измерялась амплитуда полного давления, которая отображена на графике рисунка 5.
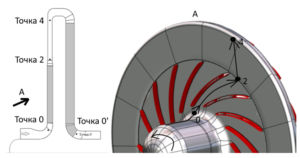
Рис. 4. Расчётная область центробежной компрессорной ступени
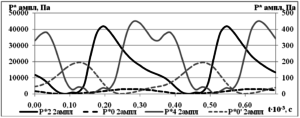
Рис.5. График удвоенных амплитуд полного давления в контрольных сечениях центробежной компрессорной ступени
Расчеты показали необходимость учета числа гармоник, которые используются в вычислениях для соблюдения условия консервативности параметров. Получены данные о различии характера течения при нестационарном и стационарном расчетах. В наши ближайшие планы входит проведение комплекса исследований с целью верификации NLH метода, оценки выигрыша в вычислительных ресурсах и времени расчета при использовании мощных суперкомпьютерных ресурсов.
Литература:
- Лопулалан, Хенри Доминггус. Виртуальный стенд для исследования нестационарных процессов в ступени центробежного компрессора [Текст]: дис. канд. техн. наук: 05.04.06 / Лопулалан Хенри Доминггус; Санкт-Петербургский государственный политехнический университет.
- He, L., “Modelling Issues for Computation of Unsteady Turbomachinery Flows,” Unsteady Flows in Turbomachines, von K´arm´an Inst. Lecture Series 1996-05, von Karman Inst. for Fluid Dynamics, Rhode Saint Genese, Belgium, March 1996.
- He and W. Ning, «An Efficient Approach for Analysis of Unsteady Viscous Flows in Turbomachinery”, AIAA Journal,Vol.36, No.11, 1998.
- Vilmin, S., Lorrain E., and Hirsch, C.: Unsteady Flow Modeling Across the Rotor/Stator Interface Using the Nonlinear Harmonic Method, ASME Paper GT-2006-90210, (2006)



